Chapter 6 Elementary Functions

Section 6.4 Exponential and Logarithmic Functions

6.4.2 Contents

In the previous example, an exponential function with base $a=2$ occurs, and the independent variable - in this example this is the variable $t$ - occurs in the exponent. We will now specify the general mapping rule for an exponential function with an arbitrary base $a$; however, we here assume $a>0$:

${\displaystyle f:\mathrm{\hspace{0.5em}\hspace{0.5em}}\{\begin{array}{ccc}\hfill ℝ& \hfill \to \hfill & (0;\infty )\hfill \\ \hfill x& \hfill ⟼\hfill & f(x)=f_0·a^{\lambda x}\hfill \end{array}}$

Here, $f_0$ and $\lambda$ denote so-called parameters of the exponential function that will be introduced below.
The domain of all exponential functions is the set of all real numbers, i.e. $D_f=ℝ$, whereas the range only consists of the positive real numbers, i.e. $W_f=(0;\infty )$, since every power of a positive number can only be positive.

Some general properties can be seen from the figure below showing exponential functions $g:ℝ\to (0;\infty )$, $x⟼g(x)=a^x$ for different values of $a$:

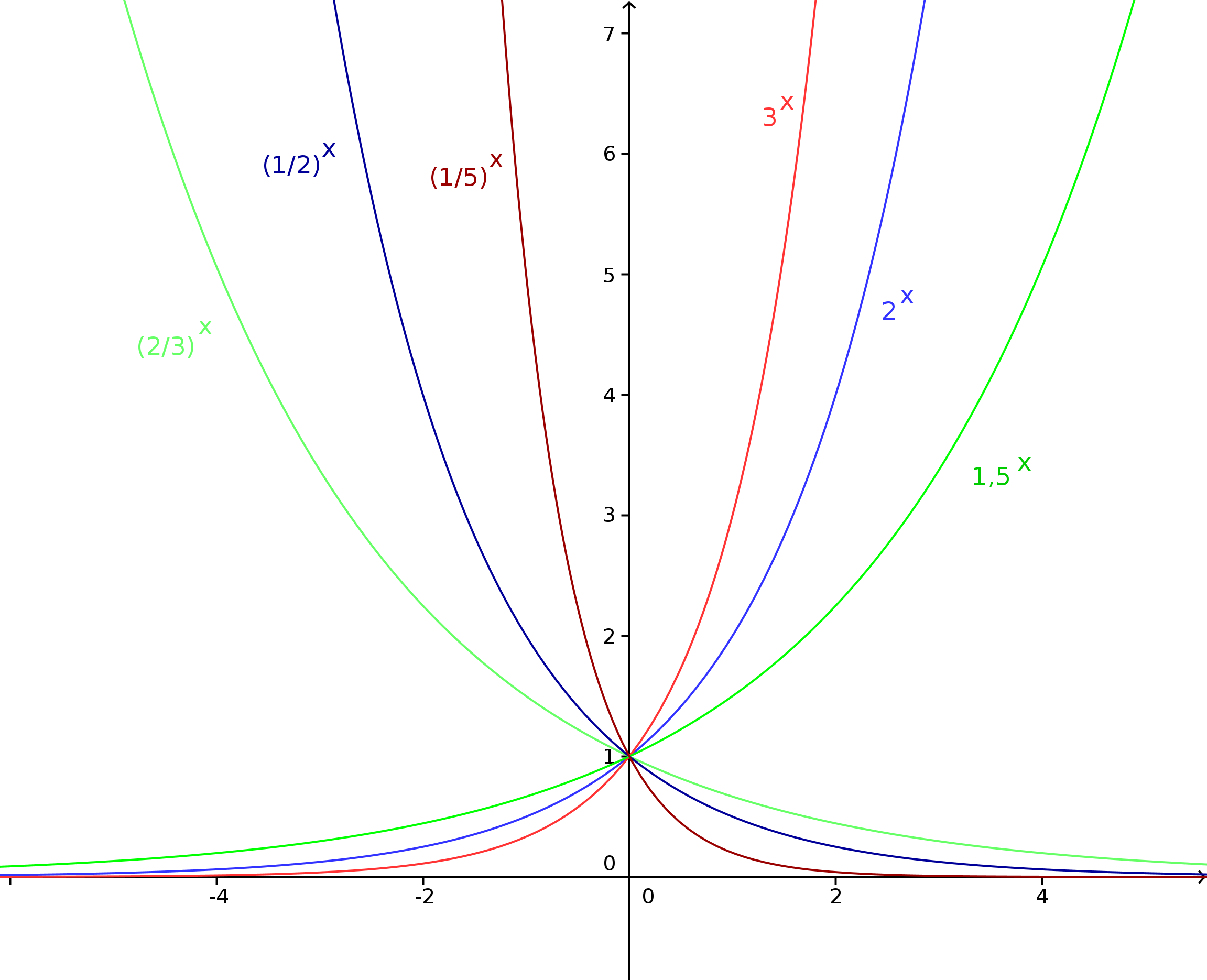
• All these exponential functions pass trough the point $(x=0,y=1)$, since $g(x=0)=a^0$ and $a^0=1$ for every number $a$.
  
• If $a>1$, then the graph of $g$ rises from left to right (i.e. for increasing $x$-values); one also says that the function $g$ is strictly increasing. The greater the value of $a$, the steeper the graph of $g$ rises for positive values of $x$. Moving towards ever larger negative values of $x$ (i.e. approaching from right to left) the negative $x$-axis is an asymptote of the graph.
  
• If $a<1$, then the graph of $g$ falls from left to right (i.e. for increasing $x$-values); one also says that the function $d$ is strictly decreasing. The greater the value of $a$, the slower the graph of $g$ falls for negative values of $x$. Moving towards ever larger positive values of $x$ (i.e. approaching from left to right) the positive $x$-axis is an asymptote of the graph.
  

What are the parameters $f_0$ and $\lambda$? The parameter $f_0$ is easily explained: if the value $x=0$ is inserted in the general exponential function $f$, resulting in

${\displaystyle f(x=0)=f_0·a^{\lambda ·0}=f_0·a^0=f_0·1=f_0\hspace{0.5em},}$

then it can be seen that $f_0$ is a kind of starting point or initial value (at least if the variable $x$ is taken for a time); the exponential progression $a^{\lambda x}$ is generally multiplied by the factor $f_0$ and thus weighted accordingly, i.e. stretched (for $|f_0|>1$) or compressed (for $|f_0|<1$).
The parameter $\lambda$ that occurs in the exponent is called growth rate; it determines how strong the exponential function - with the same base - increases (for $\lambda >0$) or decreases (for $\lambda <0$). The expression $a^{\lambda x}$ is called growth factor.