Chapter 6 Elementary Functions
Section 6.7 Final Test6.7.1 Final Test Module 6
This is a test for submission:- Unlike open exercises, no hints for formulating mathematical expressions are provided.
- The test can be restarted or interrupted at any time.
- The test can be terminated and submitted using the buttons at the end of the page, or reset.
- The test can be attempted several times. Only the last version will be included in the statistics.
Exercise 6.7.1
Specify the maximum domains and of the two functions
and
and
Exercise 6.7.2
Specify the range of the function
Exercise 6.7.3
Find the parameters in the exponential function
such that and .
Answer:
,
.
Simple logarithms can be left as they are, e.g. can be entered as ln(100) even though the exact value of is unknown.
such that and .
Answer:
,
.
Simple logarithms can be left as they are, e.g. can be entered as ln(100) even though the exact value of is unknown.
Exercise 6.7.4
Specify the composition (note: ) of the functions
and
Answer:
.
Find the parameters such that the sine wave described by the function has the graph shown below.
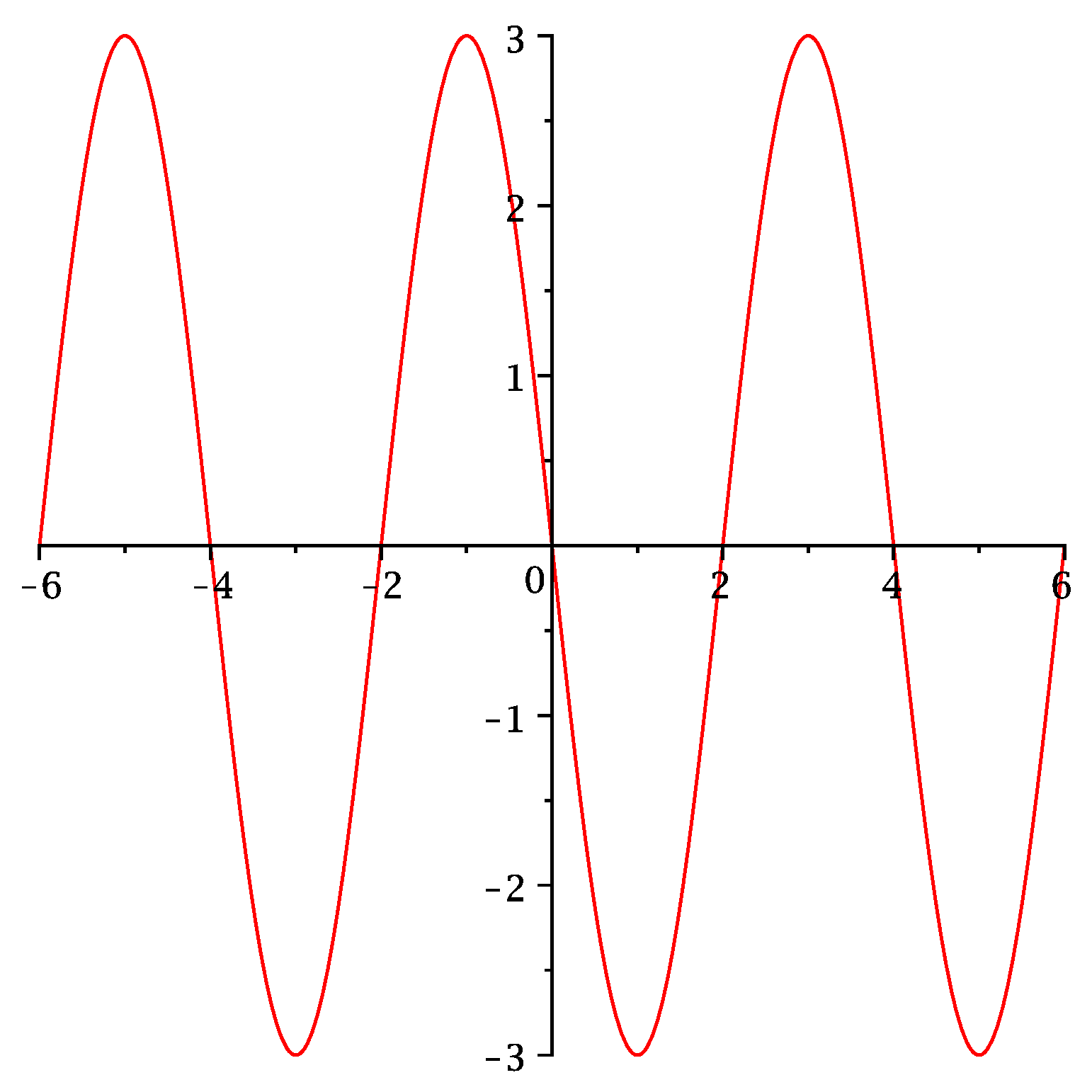
Answer:
.
and
Answer:
.
Find the parameters such that the sine wave described by the function has the graph shown below.

Abbildung 1: A sine wave.
Answer:
.
Exercise 6.7.5
Specify the inverse function of
The function has
The function has
- the domain .
- the range .
- the mapping rule .
Exercise 6.7.6
Please indicate whether the following statements are right or wrong:
The function
| ... can be also written for short as . | ||
| ... is a linear affine function. | ||
| ... has the range . | ||
| ... has the slope . | ||
| ... can only take values greater or equal and less than . | ||
| ... has a graph that is a piece of a line. | ||
| ... has at the value . | ||
| ... has the domain . |
Exercise 6.7.7
Calculate the following logarithms:
- .
- .
- .
The test evaluation will be displayed here!
 Onlinebrückenkurs Mathematik
Onlinebrückenkurs Mathematik