Kapitel 8 Integralrechnung

Abschnitt 8.2 Bestimmtes Integral

8.2.2 Integral


Das Integral einer Funktion f mit f(x)≥0 kann als „Fläche unter der Kurve“ interpretiert werden. In dem nach Riemann benannten Integral wird der Funktionsverlauf durch eine Treppenfunktion angenähert, und deren Funktionswerte werden, gewichtet mit der jeweiligen Intervalllänge bzw. „Breite einer Treppenstufe“, aufsummiert. Dies ist in der unten gezeigten Abbildung beispielhaft dargestellt.

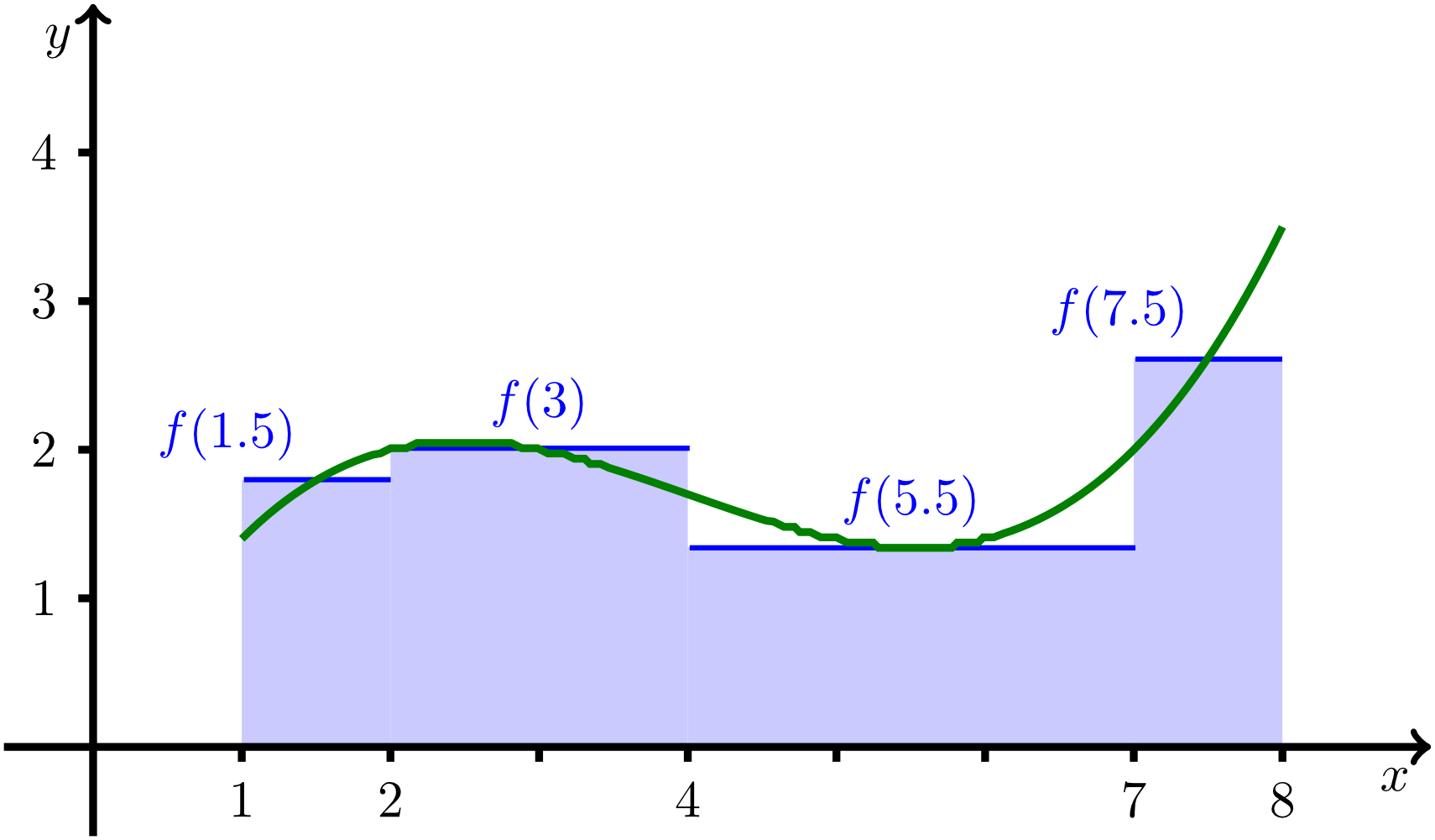
Zur Definition des Integrals: Funktion angenähert durch eine Treppenfunktion,
unterteilt in vier Teilintervalle.
Man erkennt, dass die Fläche unter der Kurve zunächst durch Rechtecke angenähert wird, deren eine (horizontale) Seitenlänge durch ein Intervall auf der x-Achse bestimmt wird, während die Länge der zweiten (vertikalen) Seite durch einen Funktionswert f( zk ) an der Stelle zk innerhalb des dazu gehörenden x-Intervalls beschrieben wird. Man bestimmt nun die Flächen dieser Rechtecke und summiert diese Teilflächen auf. Je kleiner die Intervalle auf der x-Achse werden, umso mehr nähert sich die so berechnete Summe dem „wahren“ Wert der Fläche unter der Kurve, also dem Integral der Funktion, an.
Formal heißt das, dass man eine Summe Sn der Form

Sn = ∑k=0 n-1f( zk )·Δ( xk )       mit   Δ( xk )= xk+1 - xk

bestimmt. Im betrachteten Beispiel wird das Intervall [0;8] in vier Teile eingeteilt. Dabei sind x0 =1, x1 =2, x2 =4 und x3 =7. Wendet man darauf diese Summenformel an, so erhält man

S4 = f( z0 )·( x1 - x0 )+f( z1 )·( x2 - x1 )+f( z2 )·( x3 - x2 )+f( z3 )·( x4 - x3 ) = f( z0 )·(2-1)+f( z1 )·(4-2)+f( z2 )·(7-4)+f( z3 )·(8-7) = f( z0 )·1+f( z1 )·2+f( z2 )·3+f( z3 )·1 .

Offensichtlich genügt es nicht, nur einige wenige Teilintervalle zu betrachten. Im Allgemeinen wird man die maximale Länge der Teilintervalle xk+1 - xk immer kleiner wählen müssen und damit für immer mehr Teilintervalle die Summanden f( zk )·( xk+1 - xk ) berechnen und addieren, um einen möglichst genauen Wert der Fläche zu berechnen. Deshalb betrachtet man den Grenzwert, dass die maximale Intervalllänge der Teilintervalle gegen Null geht.
Prinzipiell kann obiges Vorgehen auch auf Funktionen mit negativen Funktionswerten angewandt werden. Wie man dann den Flächeninhalt berechnet, wird im Abschnitt 8.3 erläutert. In jedem Fall sind einige Aspekte in der Definition des Integrals zu beachten, die über den Rahmen dieses Kurses hinausgehen. Deshalb wird für die Details zu den Voraussetzungen in der nachfolgenden Definition auf die weiterführende Literatur verwiesen.
Integral 8.2.1
Gegeben ist eine Funktion f:[a;b]→ℝ auf einem reellen Intervall [a;b]. Zu „feiner werdenden“ Unterteilungen des Intervalls, sodass xk+1 - xk gegen 0 geht, nennt man

∫a b f(x) dx= limn→∞ Sn = limn→∞ ∑k=0 n-1f( zk )·( xk+1 - xk )    mit    xk ≤ zk ≤ xk+1 (8.2.1)

das bestimmte Integral von f mit der Untergrenze a und der Obergrenze b (wenn der Grenzwert existiert und unabhängig von der jeweiligen Unterteilung ist), und die Funktion f heißt dann integrierbar. Die Funktion f wird in diesem Kontext auch Integrand genannt.

Prinzipiell kann es vorkommen, dass auf diese Weise gar kein bestimmter Wert berechnet werden kann, das Integral also nicht exisitert. Weiterführende Überlegungen zeigen, dass jedenfalls für jede stetige Funktion das Integral existiert. Als Beispiel wird das Integral von f:[0;1]→ℝ, x↦x berechnet, wobei die Berechnung des Grenzwertes im Vordergrund steht.
Beispiel 8.2.2
Es soll das Integral von f:[0;1]→ℝ, x↦x berechnet werden. Dazu teilt man das Intervall [0;1] am einfachsten in gleich breite Teilintervalle [ xk ; xk+1 ] mit x0 :=0 und xk := xk-1 + 1 n ein. Die Intervalllänge ist also Δ( xk )= xk+1 - xk = 1 n .
Untersucht man die Intervalllänge auf ihr Verhalten für n gegen unendlich, dann sieht man, dass Δ( xk ) immer kleiner wird und gegen Null strebt. Die Voraussetzung für die Berechnung eines bestimmten Integrals ist also gegeben.
Für die Werte xk findet man unter Zuhilfenahme der Intervalllänge außerdem xk = k n . Wählt man zk = xk für die Zwischenstellen, ergibt sich f( zk )=f( xk )= xk = k n .
Setzt man diese Ergebnisse in die Summenformel ein, dann erhält man unter der Verwendung der Formel ∑k=1 n-1k= 1 2  n(n-1), die nach Carl Friedrich Gauß auch als „kleiner Gauß“ bezeichnet wird, die Gleichung

Sn = ∑k=0 n-1f( xk )·Δ( xk )= ∑k=0 n-1 xk · 1 n = ∑k=0 n-1 k n · 1 n = 1 n2 · ∑k=0 n-1k= 1 n2 · ∑k=1 n-1k = 1 n2 n(n-1) 2 = 1 2 · n-1 n = 1 2 ·(1- 1 n ) .

Und mit limn→∞ 1 n =0 ergibt sich für das Integral

∫0 1 x dx= limn→∞ Sn = 1 2  .


Zur großen Klasse integrierbarer Funktionen gehören alle Polynome, gebrochenrationalen Funktionen, trigonometrischen Funktionen und Exponential- und Logarithmusfunktionen sowie deren Verknüpfungen.
Um Rechnungen möglichst unkompliziert durchführen zu können, sind möglichst einfache Regeln zur Integration von Funktionen nötig. Ein wichtiges Ergebnis liefert der sogenannte Hauptsatz der Differential- und Integralrechnung. Er beschreibt einen Zusammenhang zwischen den Stammfunktionen einer stetigen Funktion und deren Integral.
Hauptsatz der Differential- und Integralrechnung 8.2.3
Gegeben ist eine stetige Funktion f:[a;b]→ℝ auf einem reellen Intervall [a;b]. Dann besitzt f eine Stammfunktion, und für jede Stammfunktion F von f gilt

∫a b f(x) dx  =   [F(x)]a b   =  F(b)-F(a) .


Als einfaches Beispiel wird das bestimmte Integral der Funktion f mit f(x)= x2 zwischen a=1 und b=2 berechnet. Mit den Regeln für die Bestimmung von Stammfunktionen und dem Hauptsatz der Differential- und Integralrechnung kann man diese Aufgabe leicht lösen.
Beispiel 8.2.4
Die Funktion f:[1;2]→ℝ mit f(x):= x2 hat eine Stammfunktion F mit
F(x)= 1 3 x3 +C für eine reelle Zahl C. Mit dem Hauptsatz ergibt sich

∫1 2 x2  dx= [ 1 3 x3  + C]1 2 =( 1 3   23  + C)-( 1 3   13  + C)= 7 3  .

Wie man sieht, fällt die Konstante nach dem Einsetzen der Grenzen weg, sodass man sie in der Praxis bei der Berechnung von bestimmten Integralen bereits bei der Bildung der Stammfunktion ,,unterschlagen'' kann. Das heißt, man kann für die Berechnung des bestimmten Integrals C=0 wählen.

Die Gleichung im Hauptsatz gilt auch für jeden Zwischenwert z∈[a;b], sodass man gemäß

F(z)-F(a)= ∫a z f(x) dx

damit alle Funktionswerte F(z) berechnen kann, wenn die Ableitung F'=f und ein Funktionswert, beispielsweise F(a), bekannt sind. Hierfür sagt man auch, dass F aus der Ableitung F'=f rekonstruiert wird.
Anwendungsbeispiele zur Rekonstruktion einer Funktion F aus ihrer Ableitung F'=f werden am Ende des Abschnitts 8.3 vorgestellt.




: